Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics

Farthest-point Optimized Point Sets with Maximized Minimum Distance

T. Schlömer, D. Heck, O. Deussen

Material

Abstract

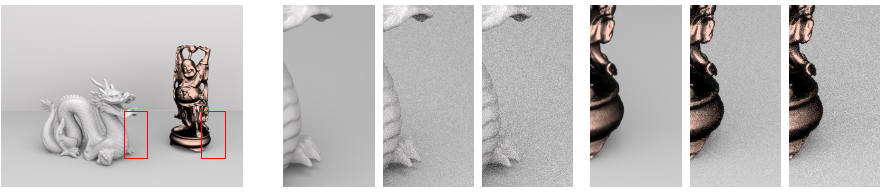
Efficient sampling often relies on irregular point sets that uniformly cover the sample space. We present a flexible and simple optimization strategy for such point sets. It is based on the idea of increasing the mutual distances by successively moving each point to the “farthest point,” i.e., the location that has the maximum distance from the rest of the point set. We present two iterative algorithms based on this strategy. The first is our main algorithm which distributes points in the plane. Our experimental results show that the resulting distributions have almost optimal blue noise properties and are highly suitable for image plane sampling. The second is a variant of the main algorithm that partitions any point set into equally sized subsets, each with large mutual distances; the resulting partitionings yield improved results in more general integration problems such as those occurring in physically based rendering.

BibTeX

@inproceedings{Schloemer2011FarthestpointOptimized,
  acmid     = {2018345},
  address   = {New York, NY, USA},
  author    = {T. Schlömer, D. Heck, O. Deussen},
  booktitle = {Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics},
  doi       = {10.1145/2018323.2018345},
  isbn      = {978-1-4503-0896-0},
  keywords  = {Delaunay triangulations, Poisson-disk, anti-aliasing, blue noise, maximized minimum distance, numerical integration, sampling, trajectory splitting},
  location  = {Vancouver, British Columbia, Canada},
  numpages  = {8},
  pages     = {135--142},
  publisher = {ACM},
  series    = {HPG '11},
  title     = {Farthest-point Optimized Point Sets with Maximized Minimum Distance},
  url       = {http://graphics.uni-konstanz.de/publikationen/Schloemer2011FarthestpointOptimized},
  year      = {2011}
}