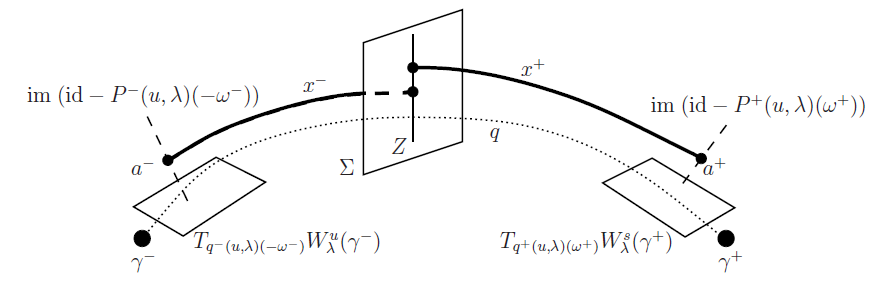
Material
Abstract
We present an extension of the theory known as Linś method to heteroclinic chains that connect hyperbolic equilibria and hyperbolic periodic orbits. Based on the construction of a so-called Lin orbit, that is a sequence of continuous partial orbits that only have jumps in a certain prescribed linear subspace, estimates for these jumps are derived. We use the jump estimates to discuss bifurcation equations for homoclinic orbits near heteroclinic cycles between an equilibrium and a periodic orbit (EtoP cycles).