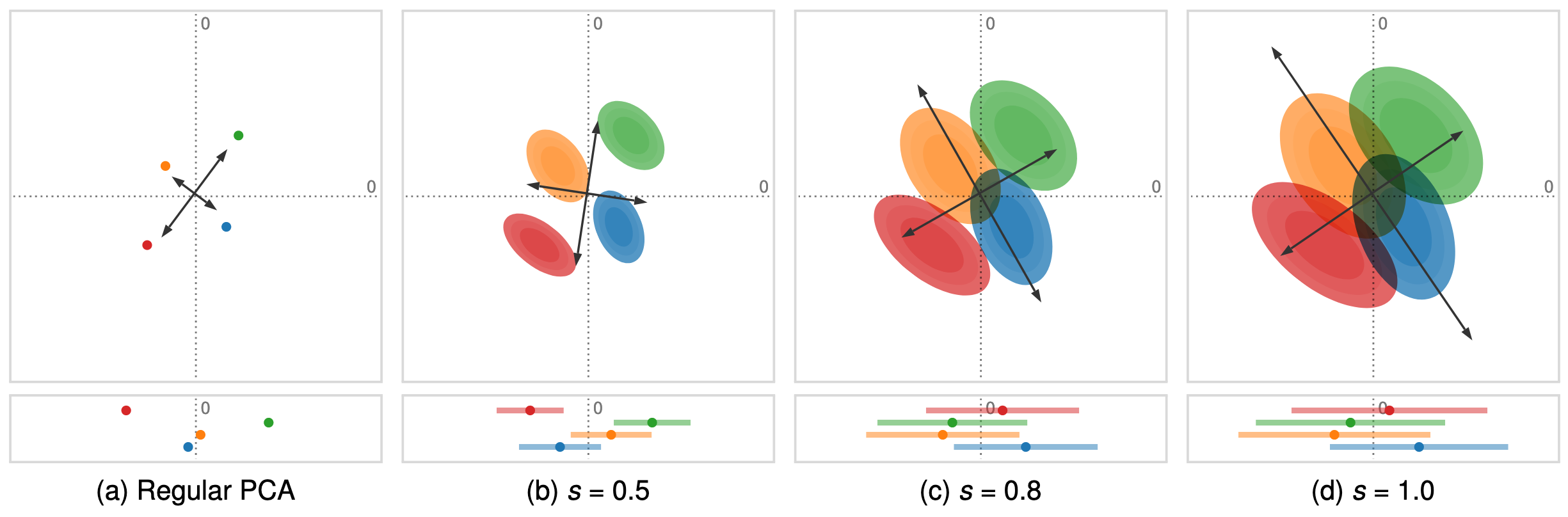
Data uncertainty can have a significant influence on the outcome of dimensionality reduction techniques. We propose ageneralization of principal component analysis (PCA) that takes into account the uncertainty in the input. The top row shows thedataset with varying degrees of uncertainty and the corresponding principal components, whereas the bottom row shows the projectionof the dataset, using our method, onto the first principal component. In Figures (a) and (b), with relatively low uncertainty, the blue andthe orange distributions are comprised by the red and the green distributions. In Figures (c) and (d), with a larger amount of uncertainty,the projection changes drastically: now the orange and blue distributions encompass the red and the green distributions.
Material
Abstract
We present a technique to perform dimensionality reduction on data that is subject to uncertainty. Our method is ageneralization of traditional principal component analysis (PCA) to multivariate probability distributions. In comparison to non-linearmethods, linear dimensionality reduction techniques have the advantage that the characteristics of such probability distributions remainintact after projection. We derive a representation of the PCA sample covariance matrix that respects potential uncertainty in eachof the inputs, building the mathematical foundation of our new method:uncertainty-aware PCA. In addition to the accuracy andperformance gained by our approach over sampling-based strategies, our formulation allows us to perform sensitivity analysis withregard to the uncertainty in the data. For this, we proposefactor tracesas a novel visualization that enables to better understand theinfluence of uncertainty on the chosen principal components. We provide multiple examples of our technique using real-world datasets.As a special case, we show how to propagate multivariate normal distributions through PCA in closed form. Furthermore, we discussextensions and limitations of our approach.